One of graphite’s primary attributes is its high degree of thermal and chemical stability, i.e., its inertness. Graphite can be thought of as being low in energy right from the start and this low chemical potential energy is the direct result of a unique bonding effect called aromaticity or resonance. Substances that exhibit resonance have a degree of chemical stability not expected. The unexpected stability is known as resonance energy.
Resonance is the result of alternating pi bonding orbitals that are present in the benzene ring structures that make up each graphene layer (keep in mind that graphite does not contain benzene). In reality the term alternating pi bonding orbitals is not really correct. Before explaining why, it would be best to first explain the structure of benzene, which is the classic model of an aromatic or resonance compound.
The Structure of Benzene
Benzene is the classic example of an aromatic molecule. Benzene is a resonance structure that has a degree of chemical stability greater than what is expected of a compound with the structure illustrated here. Note that the model pictured is a hexagonal ring of carbon atoms with alternating (conjugated) double bonds. The structure is known as the famous, or perhaps infamous, benzene ring, and is an accepted model for benzene. However, this picture does not really provide an accurate interpretation of the real benzene molecule. To illustrate this concept refer to the next Figure, which presents two different benzene molecules side-by-side.
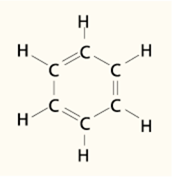
Let’s start with the left hand benzene molecule and label the carbon atoms, clockwise, from 1 to 6. Note that the double bonds are placed between the 1-2, 3-4, and 5-6 carbons. This structure is an accepted model for benzene. Now let’s move to the right hand molecule and apply the same clockwise numbering system. Note that in this molecule the double bonds have been shifted one place to the right so that they now occupy the 2-3, 4-5, and 6-1 positions.
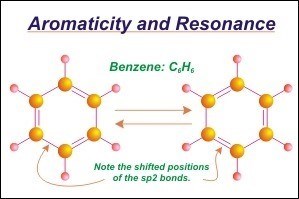
This structure is an accepted model for benzene. Note that the right hand benzene ring is not simply a 60 rotation adjustment of the left hand molecule, but is actually a new molecule which has had the bonds shifted as noted. Both structures are accepted structures for benzene, but both are different from one another. In reality neither the left nor right hand structure truly represents the benzene ring. In reality the benzene molecule is actually something in between these two structures. The structure is said to resonate between the left and right hand structure, hence the name resonance.
What actually resonates in the benzene ring are the pi bonding electrons contributed by each carbon atom. Remember that the pi electrons are not locked into position but are free to “circulate in an orbital volume created when the pi orbitals from two adjacent carbon atoms combine.” In the case of benzene, each carbon atom in the ring is sp2 hybridized so each possesses a pi electron. The result is that the overall hybridization creates a continuous pi orbital that encompasses the entire benzene ring. The pi electrons are said to be de-localized within this ring so that all six pi electrons can move around the entire molecule. The molecule resonates by virtue of the moving pi electrons.
When one considers the ball and stick Figures above, it becomes clear that the double bonds are never locked between two carbon atoms as indicated by the Figure. By virtue of the resonating pi electrons, the pi bonding orbital system encompasses all six carbon atoms at once. Each two-atom pi orbital system becomes continuous with neighboring pi orbitals with the result being a donut shaped region, existing above and below the plane of the ring where there is a high probability of finding any one of the six pi electrons. Since the integrated pi orbitals actually represent a covalent bonding connection between carbon atoms in the ring, the whole ring and its carbon atoms can be said to be double bonded. The Figure below is perhaps a better model for the actual structure of a benzene ring.
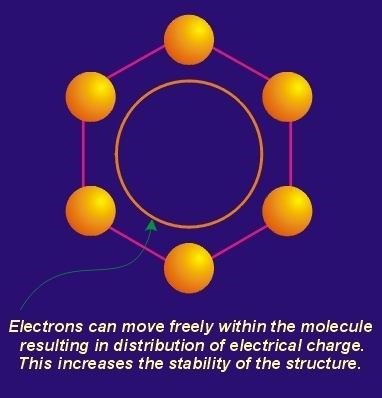
Note that in this figure the hydrogen atoms are assumed. The ring at the center of the hexagon represents the overlapping, conjugated pi orbitals. In non-quantum terms, this configuration allows the electrons to roam freely over the approximate area shown. This results in the distribution of the charge of the six electrons over a wider area than possible if they were locked in place between carbon atoms.
Resonance Energy
So what does benzene have to do with graphite? The answer to this question is the basis of why graphite is such a stable substance.
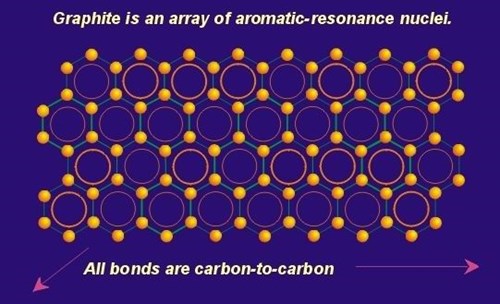
If we take a grouping of benzene rings and strip off all of the hydrogen atoms, then combine these rings on their edges the structure to the left is realized. This structure is a single graphene layer (one layer of the graphite crystal). The fusion of rings to form these layers is very possible because once the benzene gives up its hydrogen, the sp2 carbon has one free bond that can attach to another carbon from an adjacent benzene ring. Keep in mind that in this structure the conjugated pi orbitals are still maintained in each ring. Ultimately the pi systems within each ring conjugate with the pi systems in adjacent rings resulting in a continuous system that allows delocalization of electrons across the entire graphene layer (more on that below). As will be described elsewhere in this publication, this electronic arrangement is responsible for the high in-plane electrical conductivity seen in graphite.
Resonance Energy: A Quantitative View
As mentioned above, the fact that a substance exhibits resonance or aromaticity is typically associated with an increase in chemical stability. To illustrate the degree of stability the classic example of the heat of hydrogenation of benzene will be used (F.Carey 1987).

Lets make an assumption: Assume that the standard model of benzene showing a 6 carbon ring with alternating double bonds is a pinned structure, meaning that the double bonds and adjacent single bonds are locked in place as they would be in a molecule like ethene. If this substance existed (which it does not) it would be called 1,3,5-cyclohexatriene, and would look like the structure shown here.
Our goal is to measure the heat of hydrogenation of this imaginary structure and compare it to the actual heat of hydrogenation of benzene (which can be measured). The idea here is to determine which structure yields the most energy upon saturation of its double bonds with hydrogen. The structure that actually gives up more energy during this process is the one with higher chemical potential energy and therefore less chemical stability.
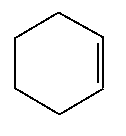
Since 1,3,5-cyclohexatriene does not actually exist, a model must to chosen to approximate its heat of hydrogenation. The model we will select will be the substance cyclohexene, C6H10, which is a six carbon ring with one set of double bonds across which the hydrogenation will occur. A schematic picture of a cyclohexene molecule is shown here. In order to approximate the hydrogenation of the three sets of double bonds found in 1,3,5-cyclohexatriene, we will perform the hydrogenation on three separate molecules of cyclohexene and assume that the approximate heat of hydrogenation of 1,3,5-cyclohexatriene is equal to three times the heat of hydrogenation of cyclohexene. These assumptions are reasonable.
The measured heat of hydrogenation of benzene (total saturation of all carbons to form cyclohexane) is approximately 50 kilocalories per mole. The heat of hydrogenation of a single cyclohexene molecule is approximately 29 kilocalories per mole. Using the proposed model, the total heat of hydrogenation of the imaginary compound 1,3,5-cyclohexatriene is equal to: (3 moles C6H10 ) X (29 kcal/mole) = 87 kcal.
So the heat of hydrogenation of our imaginary model compound is 87-kcal/mole, while the actual measured heat of hydrogenation of benzene is only 50-kcal/mole. The resonance energy can now be quantified by observing the difference in the heat of hydrogenation of the model compound compared to the real benzene molecule:
ΔHH2 Resonance = ΔHH2 1,3,5-cyclohexatriene – ΔHH2Benzene = Resonance energy
= 87 kcal/mole 50 kcal/mole = 37 kcal/mole (A significant amount of energy!)
The difference between the ΔHH2 of the two compounds is approximately 37-kcal/mole. This significant energy is the resonance energy and represents the actual increase in chemical stability realized by the benzene molecule.
So what does all this have to do with graphite? A single graphene layer is made up of millions of benzene ring structures and each of these is resonance stabilized. That means the resonance energy is common to the entire graphite structure. Graphite owes part or most of its low chemical potential energy to the fact that it is a pure sp2 carbon, resonance stabilized substance

